動態規劃 Dynamic Programming

前言

小明是一名熱愛解決難題的大學生，他正在參加一個程式比賽。這次比賽有一道題目是關於動態規劃法的，要求參賽者找到一個數列中最大的連續子數列和。

動態規劃法

這邊先記幾個關鍵字 “儲存”,”小問題”,”組合”,”大問題”。所以基本上一個問題假如能符合以下就可以使用動態規劃來思考。

• 可以拆成很多小問題
• 答案可以透過組合小問題來解
• 小問題重覆量很高

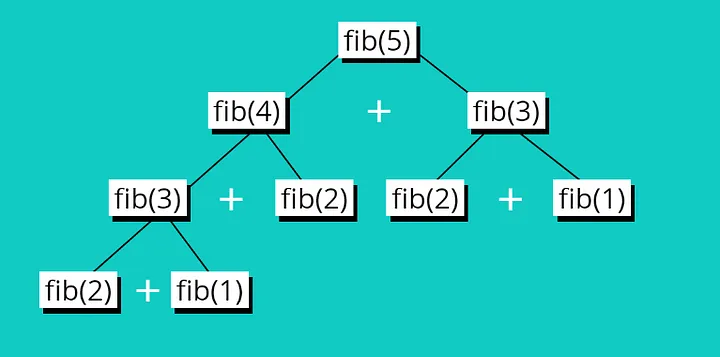
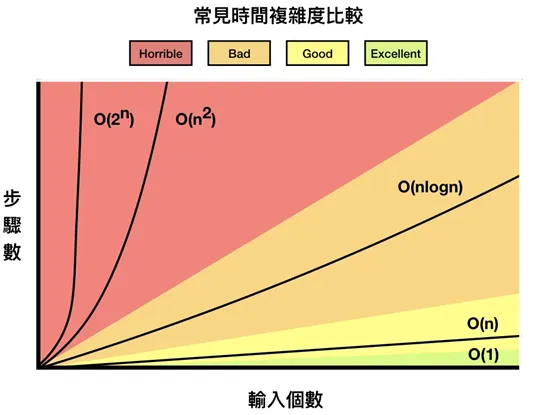
我個人研究出當有提到 subarray、subsequence 的時候也可能會使用到動態規劃。

範例

就延續前言的故事，來解最大子數列和吧！
稍微說明一下題目：在一維的數列中，要找出連續的子數列，且該子數列的和是最大。

array = [−2, 1, −3, 4, −1, 2, 1, −5, 4]

暴力解

最直覺的做法，就是直接寫一個雙層迴圈，跑完所有子數列，比較總和大小，就得出答案了。

function findMaxSubarray(array) {
  let finalMax = 0;
  for (let i=0; i<array.length; i++){
    let currentMax = 0;
    for (let j = i; j<array.length; j++){
      currentMax +=  array[j];
      if (currentMax > finalMax) {
        finalMax = currentMax;
      }
    }
  }
  return finalMax
}

另外，也附上 Wiki 的網址可以參考 連結在此

與貪婪演算法

總的來說，貪婪演算法和動態規劃算法都是求解最優化問題的重要算法。選擇哪種算法取決於問題的性質和細節，以及算法的效率和準確性要求。對於某些問題，貪婪演算法可能會得到次優解或不可行解，而動態規劃算法可以得到最優解；但是對於某些問題，貪婪演算法的效率更高，而動態規劃算法需要額外的空間和時間來求解。因此，在選擇算法時，需要根據問題的特點和要求來選擇適合的算法。

有關動態規劃的題目

• 斐波那契數列
• 連續子數列最大和 Leet Code 53
• 連續子數列最大乘積 Leet Code 152
• 最長遞增子數列 Leet Code 1143
• 數組數列中，最長子數列 Leet Code 115

以上圖片下載自google