『 資料結構 』圖形 Graph

前言

大家好～ 在文章開始之前，我們先讓各位看一下名詞提要。

• 頂點 Vertex or Node
• 邊 Edge：兩個頂點間的連線
• 無向性 Undirected：邊無方向性，表示兩點之間為雙向關係。 / 有向性 Directed：邊有方向性，表示兩點之間為單向關係。
• 加權 Weighted：邊加上權重，代表兩點之間的關係；點加上權重，代表狀態

以上都是我們在圖形這個章節會時常看到的名詞，那我們正是開始囉 GoGo。

範例

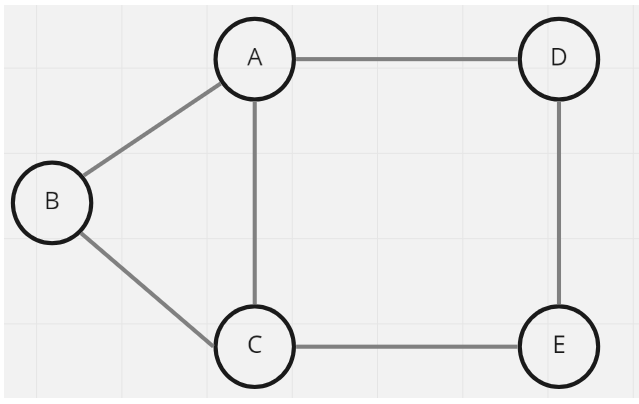
1. 無向圖
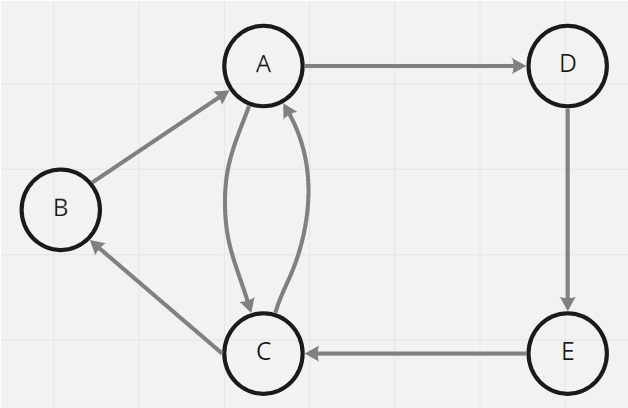
2. 有向圖
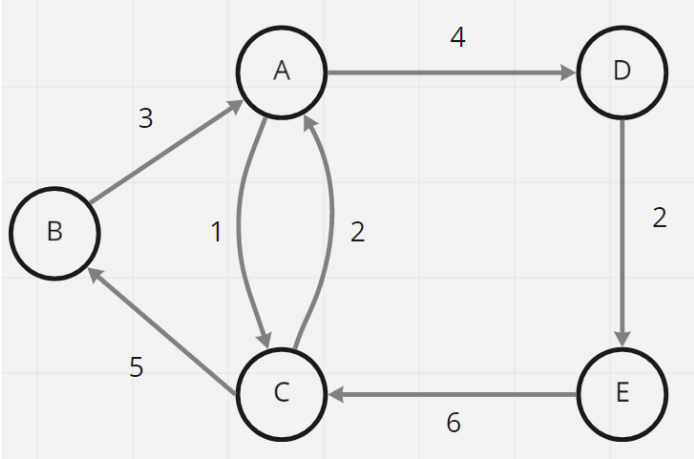
3. 權重圖

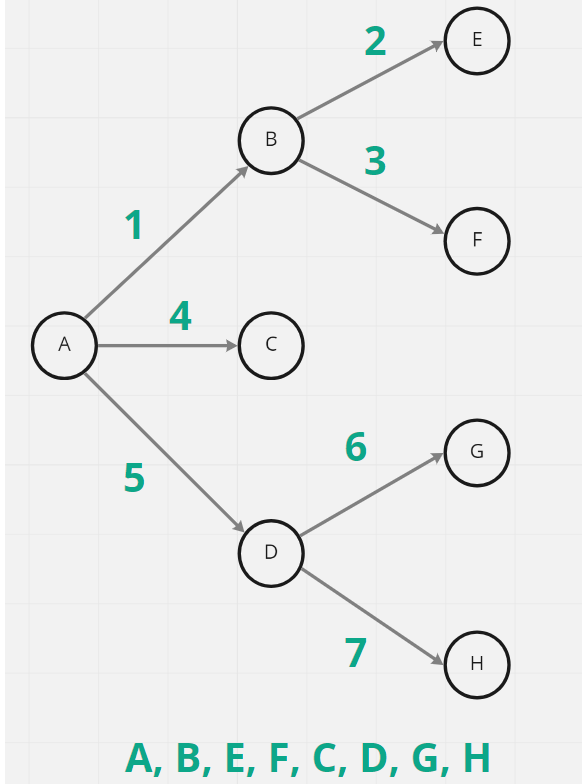
圖形遍歷 Graph Traversal

廣度搜尋 Breadth First Search

廣度優先的搜尋順序會是先走訪相鄰節點，都走訪完了，就往下一層繼續走訪，廣度優先搜尋採用queue來實作，因為queue具有先進先出的特性，可以確保先搜尋到的節點，會優先成為下一個搜尋起點。

程式範例：

class UnweightedGraph{
    constructor(val) {
        this.value = val;
        this.neighbors = [];
        this.visited = false;
    }
    addNeighbor(n) {
        this.neighbors.push(n);
    }
}

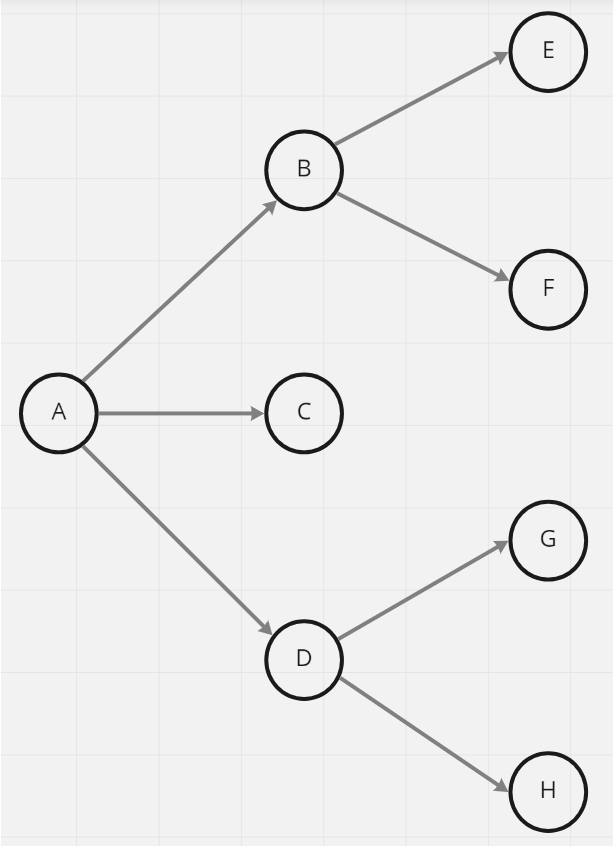
let A = new UnweightedGraph("A");
let B = new UnweightedGraph("B");
let C = new UnweightedGraph("C");
let D = new UnweightedGraph("D");
let E = new UnweightedGraph("E");
let F = new UnweightedGraph("F");
let G = new UnweightedGraph("G");
let H = new UnweightedGraph("H");
A.addNeighbor(B);
A.addNeighbor(C);
A.addNeighbor(D);
B.addNeighbor(E);
B.addNeighbor(F);
D.addNeighbor(G);
D.addNeighbor(H);

const BFS = (starter) => {
  let queue = [],
    result = [];
  queue.push(starter);
  while (queue.length !== 0) {
    let firstNode = queue.shift();
      if (!firstNode.visited) {
    firstNode.visited = true;
        result.push(firstNode.value);
        firstNode.neighbors.forEach((element) => {
          if (!element.visited) {
      queue.push(element);
    }
   })
  }
 }
 return result;
};

BFS(A);
//輸出結果 ["A", "B", "C", "D", "E", "F", "G", "H"]

深度搜尋 Depth First Search

會先從一邊開始走訪，概念類似於走迷宮摸著牆走的概念，走到底了就折返，繼續往沒走過的節點探索

程式範例：

let result = [];
const DFT = (starter) => {
    starter.visited = true;
    result.push(starter.value);
    starter.neighbors.forEach((element) => {
        if (!element.visited) DFT(element);
    });
    return result;
};

DFT(A);

//輸出結果 ["A", "B", "E", "F", "C", "D", "G", "H"]

延伸

最短距離

延伸一

延伸二

延伸三